TempoRL - Learning When to Act

Getting the best out of RL by learning when to act.

NOTE: We are using pyscript for the example below. Loading might take a bit longer.

$\color{gray}\color{gray}\mathcal{Q}$-learning:
vanilla TempoRL Skip:

Eval Speed: 50%
Eval every 10 episode(s) Env:
Training Episodes:

Avg. Train Reward:

Temporal Action:

TempoRL Demo using tabular agents. Play around to see how a TempoRL $\color{gray}\mathcal{Q}$-learning agent behaves compared to a vanilla one. Agents always start in the blue field and need to reach the orange field where they get a reward of $\color{gray}+1$. Falling down the cliff, i.e. black squares results in a reward of $\color{gray}-1$. Otherwise, the reward is always $\color{gray}0$. An episode is at most $\color{gray}100$ steps long. *Avg. Train Reward* shows the average training reward over the last $\color{gray}100$ episodes. The agents use a fixed $\color{gray}\epsilon$ of $\color{gray}0.1$. The maximal $\color{gray}\mathcal{Q}$-values are overlayed in green. The brighter the shade, the higher the value.

Reinforcement Learning (RL) is a powerful approach to train agents by letting them interact with their environment . Typically, this happens by letting the agent observe the current state of their environment. Based on this observation the agent then reacts, which results in an update to the environment which also might produce a reward or cost signal. The reward can then be used to reinforce desired behaviours, or, likewise, discourage bad behaviours. However, by only reacting to observations, agents do not learn when it is necessary to make a new decision. In our ICML’21 paper we explored a more proactive way of doing RL.

Why Should RL Agents be More Proactive?

An agent that does not only react to change in the environment, but actively anticipates what will happen, can quicker learn about consequences of their actions. This could improve learning speeds as agents would only need to focus on fewer critical decision points, rather than having to try and handle every observation the same. Further, a proactive agent is capable of more targeted exploration as the agent can commit to a plan of action for regions where it is certain until it requires replanning and exploration in less frequently visited areas. Finally, proactive agents are also more interpretable by not only stating which action to take in a state but also predicting when new decisions need to be made. This allows us to better understand the learned policies and, potentially, the underlying MDPs.

Take a look at the example at the top of this post to verify these claims for yourself. The example provides simple tabular $\color{gray}\mathcal{Q}$-learning agents on environments with sparse rewards. If you select the vanilla version, you will train a standard agent. Our more proactive TempoRL agent can jointly learn how long an action should be repeated when it is played in a state. You can set the maximal repetition value. While all environments can be used to verify the claims above, you might observe the biggest differences on the EmptyField environment. Our TempoRL agent will quicker find a successful policy, by quicker backpropagation of the observed reward values. Further, the environment gets explored more thorough and the learned action repetition tells us that the agent views most states as equivalent such that it only needs to make few decisions to reach the goal.

How to Train Proactive RL Agents

To get to a more proactive way of RL, we proposed to jointly predict which action to take in a state and how long the action should be played. Our method TempoRL, counter to prior methods (see, e.g., 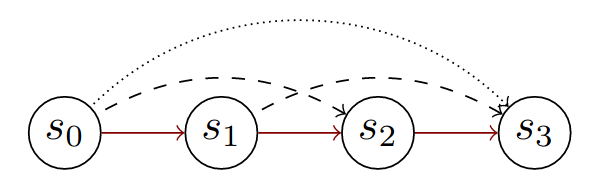) crucially conditions the repetition value in a state on the intended action. Thus, a TempoRL agent can target action repetition only for those actions in a state that actually benefit from action repetition. Further, through the use of action repetition we can quickly back propagate reward information. If we decide to repeat an action $\color{gray}N$ times, then we are able to learn about all smaller skips in between as well. Thus, we can very quickly observe if action repetitions is worth it and for how long an action should be repeated. An example of this is given in the following figure.

Observed action repetitions when committing to a larger repetition value. When repeating an action for 3 steps, we can also observe the value of repeating the same action for two steps (starting in different states) as well as playing the action only once (starting in different states).

Thus, we can quickly learn the repetition through n-step updates whereas we learn the action value through normal 1-step updates.

TempoRL

In this post we will spare you the details of how to implement TempoRL. To get an intuition of how TempoRL behaves we encourage you to go ahead and play with the demo on top. We suggest that you let the agents train for longer but frequently evaluate their performance to get an understanding for how the reward information is propagated. Quite quickly you might see that our TempoRL method finds a successful policy much quicker than the vanilla agent. You should see that, along the path of the successful policies, reward information is quickly back propagated and that TempoRL can then, over time, refine the policy to the optimal one. Counter to that, the vanilla agent, with its one-step exploration and backup, is only capable of slow backpropagation and explores a fairly small area.

In the following we will show some of the results from our paper. However, this is only a brief summary of the results and there is much more to find in our paper.

Tabular Agents

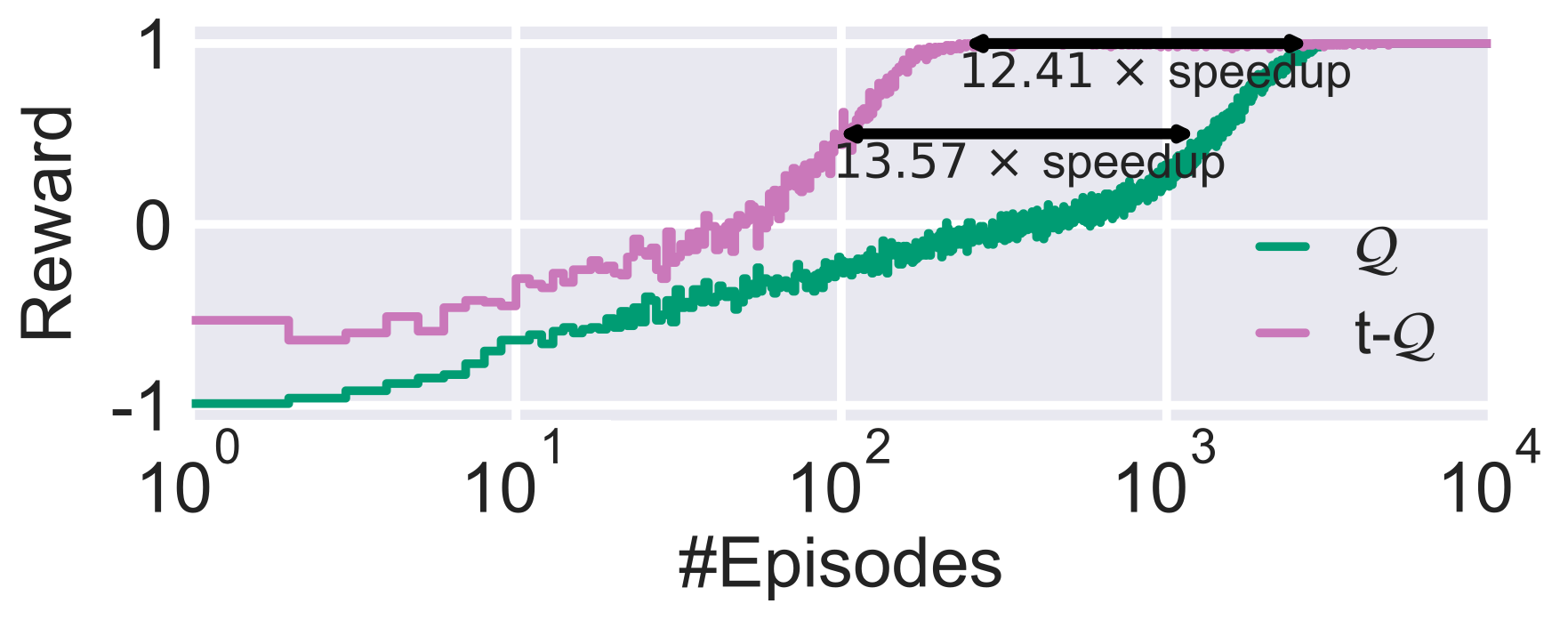
Comparison of a Tabular $\color{#508d7c}\text{vanilla }\mathcal{Q}\text{-learning}$ agent vs. our $\color{#9f7499}\text{TempoRL }\mathcal{Q}\text{-learning}$ agent on the *Cliff* environment from above. Results are averaged over 100 random seeds.

We first evaluated TempoRL for tabular RL agents. The result of which you can play with at the beginning of this post. We observed large improvements in terms of learning speeds (see the previous figure for an example). Further, our results showed that TempoRL is robust to the choice of maximal repetition value (i.e. the skip value). However, the larger the skipping value, the more options our TempoRL agent needs to learn with. For much too large skipping values this can start to slow down learning before action repetition can be used effectively.

Deep RL Agents

TempoRL is not limited to the tabular setting. To make it work in the deep case, we evaluated different architectures that make it possible to use TempoRL for featurized environments (i.e. environments with vector representation of states) as well as pixel-based environments. For details on the architectures we refer to our paper. As example, we trained the popular DQN method on different Atari games.

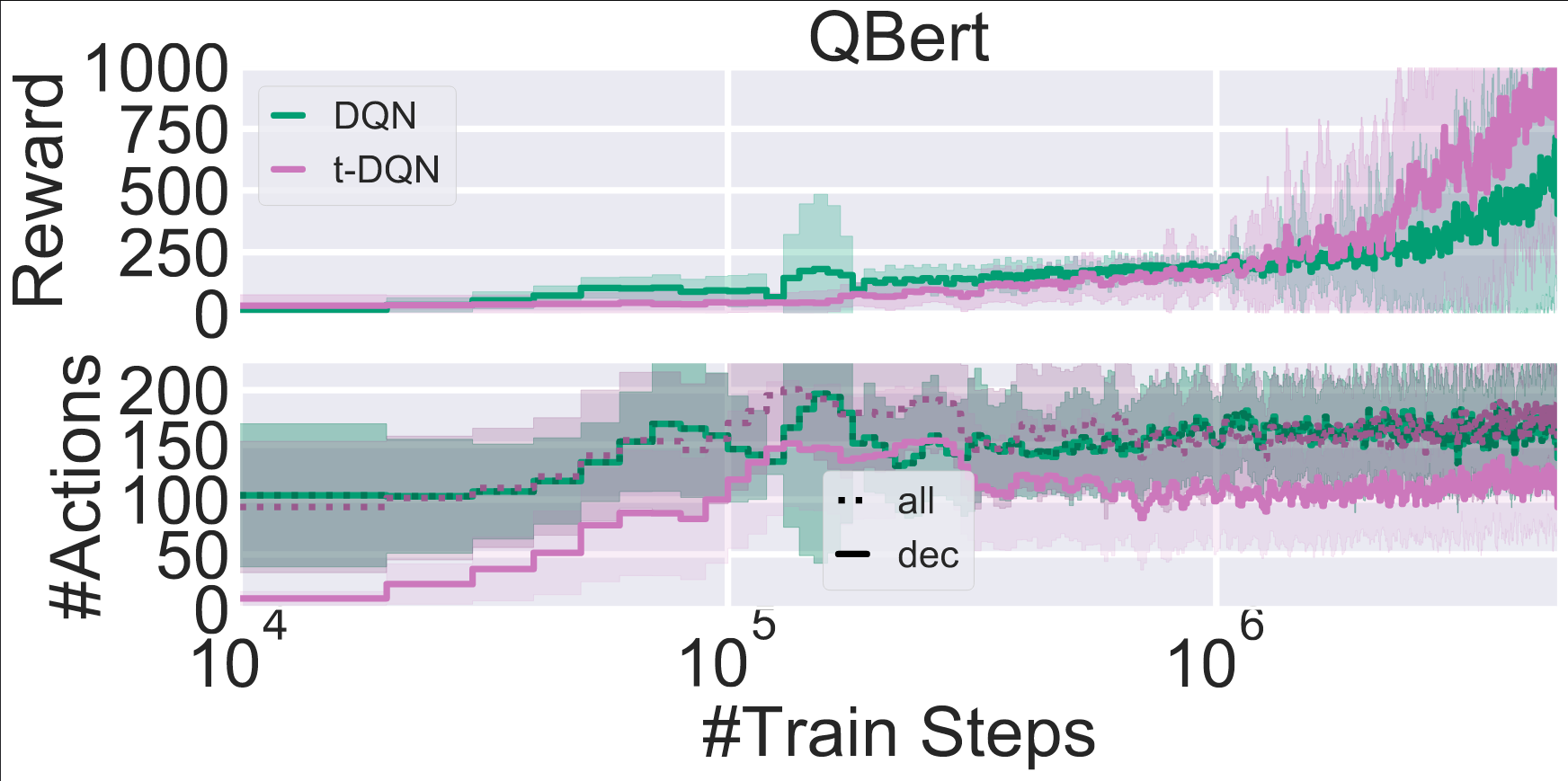
Comparison of a Tabular $\color{#508d7c}\text{DQN}$ agent vs. our $\color{#9f7499}\text{TempoRL DQN}$ agent on the Q*bert Atari environment as part of ALE. Results are averaged over 15 random seeds. The top plot gives the evaluation reward and the bottom plot the total number steps per evaluation episode (all) as well as the number of required decisions (dec).

On Q*bertFor details on the game see https://en.wikipedia.org/wiki/Q*bert we could observe that TempoRL first needed to learn the value of repeating actions. Thus, in the beginning the performance of the TempoRL agent is lagging behind that of the vanilla DQN agent. Once TempoRL has learned to make correct use of action repetition however, it speeds up learning dramatically and outperforms the baseline agent.

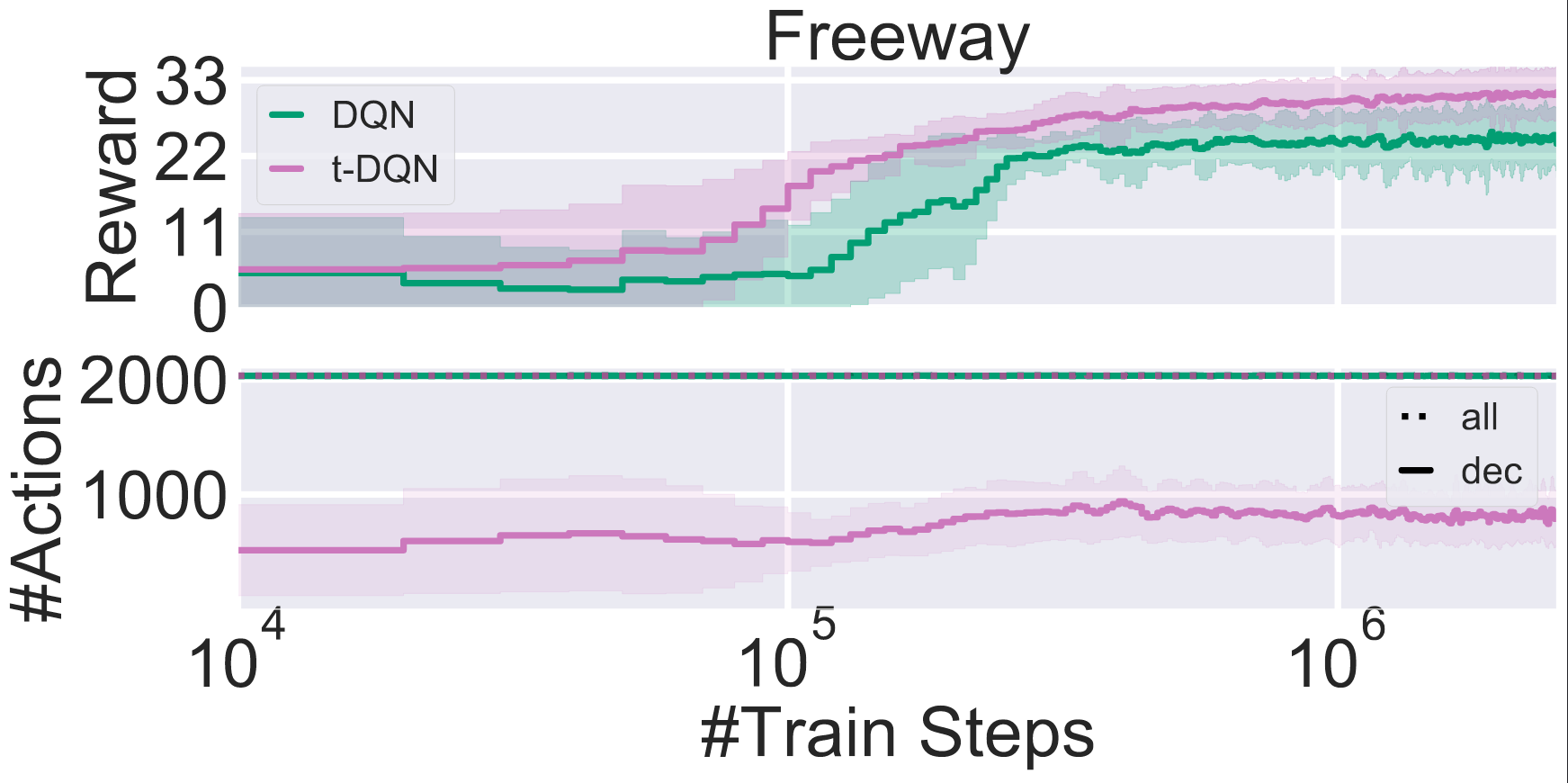
Comparison of a Tabular $\color{#508d7c}\text{DQN}$ agent vs. our $\color{#9f7499}\text{TempoRL DQN}$ agent on the freeway Atari environment as part of ALE. Results are averaged over 15 random seeds. The top plot gives the evaluation reward and the bottom plot the total number steps per evaluation episode (all) as well as the number of required decisions (dec).

A second environment worth mentioning is freewayFor details on the game see https://en.wikipedia.org/wiki/Freeway_(video_game). Here, an agent is tasked with clearing a busy freeway. To do so, agents will have to frequently repeat the UP action, only needing to stop to avoid collisions with oncoming cars. Our results show that in this environment our TempoRL method can drastically reduce the required number of decisions by the agent, thereby not only increasing the learning speed, but also learning better policies that reliably solve the environment, clearly outperforming the baseline agent.

TempoRL however, is not only limited to $\color{gray}\mathcal{Q}$-learning methods. TempoRL can work with any value based agents. For example, in the paper we further evaluated TempoRL together with a DDPG agent. Again, for details we refer to the paper.

Conclusion

We presented TempoRL, a method for more proactive RL agents. Our method can jointly learn which action to take and when it is necessary to make a new decision. We empirically evaluated our method using tabular and deep RL agents. In both settings we observed improved learning capabilities. We demonstrated that the improved learning speed not only comes from the ability of repeating actions but that the ability to learn which repetitions are helpful provided the basis of learning when to act. Our demo at the top of the post lets the reader confirm these claims themselves.

This post is based on our ICML 2021 paper TempoRL: Learning When to Act. The code for the paper is available at https://github.com/automl/TempoRL. If you find any issues in this post, please create an issue on github.